Baseline linear time-series models
As a baseline comparison for wavelets and fractal analysis, the research analyzed the price time series for each of the 10 most popular NFTs using ARIMA models to assess the method which extracts the greatest amount of information. If Elliott Wave or fractal theories of price series are valid, then they should outperform our baseline series.
I denote the observed NFT price series by \(p_{1} ,p_{2} ,…,p_{n}\). A forecast of \(p_{t + h}\) based on all of the data up to time \(t\) is denoted by \(\hat{p}_{t + h|t}\). Figure 7 graphically shows ARIMA forecasts of each of the top 10 NFT price streams over the span of the dataset and Table 3 shows fit statistics. For each price stream, the auto.arima algorithm in R’s forecast package computed the optimal \(ARIMA\left( {p,d,q} \right)\) model, where \(p\) is the order (number of time lags) of the autoregressive model, \(d\) is the degree of differencing (the number of times the data have had past values subtracted), and \(q\) is the order of the moving-average model based on the fit statistics in Table 3. In all cases, ARIMA forecasting performed only as well as a random forecast, and ARIMA models were determined not to provide good models of NFT price behavior.
Fractal behavior in the NFT price series
Elliott Wave theory is claimed to provide a fractal-like method for predicting the length and frequency of ‘bull’ and ‘bear’ market swings, perceiving a recursive ‘fractal’ price structure in asset markets43. Elliott’s work as been a factor in related studies of asset price time and frequency resolution71,72,73,74. Until recently, fractal algorithm implementations have been unavailable for analyzing large price datasets such as the one used in this research.
The current research analyzes the multifractal spectrum of Hurst exponents H of the price series, a measure of long-term memory of time series, using R’s MFDFA83 package. For self-similar time series (e.g., Elliott waves) H is directly related to fractal dimension, D, where \(1 < D < 2\), such that \(D = 2 – H\). The values of the Hurst exponent vary between 0 and 1, with higher values indicating a smoother trend, less volatility, and less roughness84. A multifractal system is a generalization of a fractal system in which a single exponent (the fractal dimension) is not enough to describe its dynamics; instead, a continuous spectrum of exponents (the so-called singularity spectrum) is needed85. Multifractal systems are common in human behavior and elsewhere in nature. They include the length of coastlines, mountain topography, fully developed turbulence, real-world scenes, heartbeat dynamics, human gait and activity, human brain activity, and natural luminosity time series.
In a multifractal system the behavior around any point is described by a local power law \(s\left( {q + a} \right) – s\left( q \right) \sim a^{h\left( q \right)} .\) The exponent \(h_{q} = h\left( q \right)\) is called the singularity exponent, as it describes the local degree of singularity or regularity around the point \(q\). Multifractals tend to be scale invariant yielding power-law behaviors, self-similarity, and multiscaling86. The curves \(\left[ {D_{q} ,h_{q} } \right]\) (such as shown in Fig. 8) are called singularity spectra and fully describes the statistical distributions of the price series.
Were the fractal perspective of Elliott Waves to be correct, we would expect each of the top 10 NFTs to have the same singularity spectrum, one that is defined by the Elliott Wave behavior of five upward steps and three downward steps at multiple scales. In fact, each of the singularity spectra in Fig. 8 define significantly different spectra, and thus different behavior in the markets for the 10 most traded NFTs. Fractal analyses of NFT price series do not show consistent, comparable fractal behavior for different NFTs, and thus is not suitable for prediction of future price series based on prior behavior.
Wavelet decomposition as a method of identifying Elliott Wave and Fractal behavior
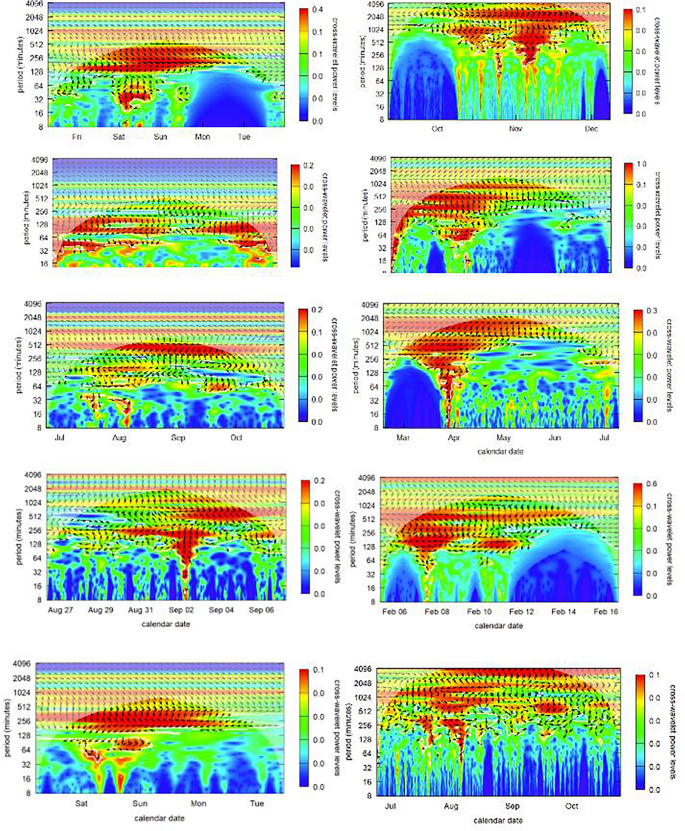
Wavelets analyze data in a time–frequency domain, rather than just frequency (as with Fourier analysis), or time (as with ARIMA), and offer a comprehensive mathematical model in that domain. Wavelets hold the potential for extracting specific causal relationships that occur repeatedly over limited time-periods, and which are predictable, repeatable and systemic. Thus they appear to be a very promising candidate for rigorously modeling Elliott waves in price series, which are claimed to reflect investor group psychology. Wavelets are able to fully model patterns, such as those claimed in Elliott wave theory, that appear at multiple scales with neither beginning nor ending. The software and computing power available before a decade ago was inadequate for a thorough study of Elliott waves, which is likely one reason that so few studies have yet taken this approach. Analysis by the many adherents who have invested time and money in understanding Elliott wave patterns has up to this point been implemented using either linear models or using Fibonacci sequences, both computationally less intensive approaches. The current research analyzed wavelets using R’s WaveletComp87 package, which was able to fully capture the salient features of Elliott wave theory. Figure 9 shows the price timeseries for the top 10 NFTs analyzed in this research.
The graph in Fig. 10 analyzes autocycles in the price series of each of the top 10 NFT analyzed in this research. We would expect Elliott Waves to present themselves as autocycles (comparable to autocorrelations) on one of the power spectra, i.e., the color corresponding to the scale at the right at a particular periodicity on the y-axis. The minute-by-minute price series of each of the top 10 NFT was analyzed to compute their power spectra between each possible set of two points on the price series, i.e. their autocycles. The important features of intraday trading are captured in the chosen periodicity time scale which span from 4 min to about 8 h (512 min). Longer weekly cycles were found for all of these NFTs, but these are artifacts that are common for most asset price series. There is very little activity before the end of 2019 in any of these NFTs. Where there were significant autocycles in pricing (the red “high power” funnels) spanning all periods that would appear randomly in time. These reflect times where specific NFTs were being strongly promoted and where there was significant media hype around the particular NFT.
Though there were between three and nine brief periods of high volume, highly autocorrelated activity in each of the NFT price streams, there were no dates that were consistent across all of the price streams. Individual NFTs exhibited their own specific idiosyncratic price autocycles.
The graphs in Fig. 11 show the analysis of general autocyclic power of the Ether, Bitcoin and the whole NFT market. These were small and power spectra are uninformative, supporting a common assertion that prices are statistically independently distributed over time. The next section looks at interactions between cryptocurrency and NFT prices. The current research found that Ether price had little influence on NFT prices, even though NFTs on the OpenSea platform were almost always implemented on the Ethereum blockchain.
I concluded from these analyses that price behavior is strongly tied to the asset and its community of fans/traders. These traders will exhibit periodic idiosyncratic bouts of trading which cools for a while, and then restarts. But wavelet analysis provides no discernible indication of Elliott Wave behavior across the full price series of any of these NFTs.
Trading interactions between cryptocurrencies and individual NFTs
Prior research49 asserted that when Bitcoin and Ether experienced large price and volume movements, NFT prices and trading volume also tended to rise or fall. Additionally, NFT prices were significantly higher when the market sentiment was positive, as measured by the Crypto Fear and Greed Index. NFT traders displayed hedging behavior, as they tended to sell NFTs and move into Bitcoin or Ether during periods of high volatility or uncertainty in the cryptocurrency markets, suggesting that NFT traders might use Bitcoin and Ether as a hedge against market risk. If hedging49 into and out of Ether and Bitcoin exists in NFT markets, then they should show up in wavelet analysis. Wavelets offer an alternative to the direct causality of econometrics, by additionally providing lead and lag information embedded in the phase difference between the two variables. Wavelets analyze time in terms of coherency, start, duration and phase. Phase can be though of in terms of causality plus a time (lead-lag) component. No cause and effect relation is instantaneous—even physical systems’ cause effect is limited to the speed of light (e.g., gravitational attraction). Phase adds the time component to causality, and essentially extends empirical analysis of causality by adding temporal information.
The graphs in Figs. 12 and 14 analyze these cryptocurrency-NFT price series couplings for of each of the top 10 NFT analyzed in this research. They generally support prior findings for price cycles of more than one trading day (i.e., 8 h) and provide detail on the nature of hedging behavior. Ante’s49 suggests that such coupling would be significant, and though this seems to be borne out at longer periodicities, it is nonexistent for periods shorter than a day (i.e., 8.5 h or 512 min). A useful analogy for understanding wavelet coherency is music’s “call and response.” In call and response, a group chorus (e.g., the market collectively) sings a motif, possibly with chordal accompaniment, and a few beats later, a soloist (e.g., an investor/trader) responds in answer. Call and response, occurs over multiple pitches (frequencies or periodicities) over multiple beats (varying time periods). Each of the powers of 2 represents an ‘octave’ and a resolution of \(\frac{1}{12}\) was used on the y-axis. Wavelet coherency of a time series in is analogous to the coefficient of correlation \(\rho\) in linear statistical models. That “call and response” appears at long intervals in Figs. 12 and 14, but not in intraday trading.
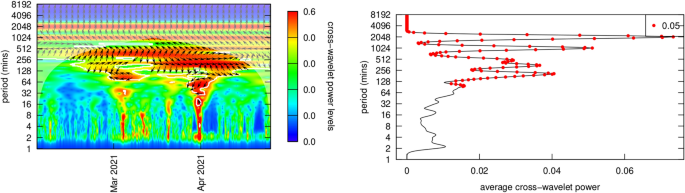
The next two sections look at NFT-cryptocurrency coherencies for Bitcoin and Ether. Because most NFTs are traded on the Ethereum blockchain, and most trades are in Ether cryptocurrency, I investigated cycles in Ether cryptocurrency, and later, coherence between Ether cycles and the top three “art” NFTs. Post-Everydays, Ether autocycles appear around 2048, 1024 and 256 min cycles (around 32 h, 17 h and 4 h). In contrast, Bitcoin dominates cryptocurrency markets and is somewhat of a de facto numeraire commodity, and thus the same analysis was applied to Bitcoin (Fig. 14). Across its full range, cycles appear around 2048 and 1024 min cycles (1.5 days and 16 h).
Ether
NFT-Ether coherency is graphed in Fig. 12. Note that in Fig. 12 and also in Fig. 14, the x-axis time values show various ranges and are not consistent. These graphs do not all cover the same time period, but for the NFT-cryptocurrency coherency analysis this was not important, as only the periodicity of the NFT-cryptocurrency relationship is being elicited. Figure 12’s cross-wavelet coherency power spectra generally supports Ante’s49 conclusions, but provides significantly more detail on how these take place in practice. Ethereum was the first blockchain to support smart contracts, and because of that, the first to support NFTs. Almost all NFTs are traded on the Ethereum blockchain, thus analysis was restricted to the Ethereum blockchain.
Inspection of coherency power spectra between Ether and the top 10 NFTs reveals common patterns in trading:
-
The black arrows on the diagram indicate the phase \(\omega\) of the coherency with trading from Ether into the NFT (generally right-pointing arrows) and out of the NFT (generally left-pointing arrows) with the degree of rotation indicating lead-lag times dependent on the period (y-axis)
-
At periods greater than 48 h (2880 min) coherency is low, implying that trade decisions are generally made within a daily time frame.
-
At periods greater than 24 h (1440 min) and less than 48 h there is significant into and out of Ether and that specific NFT, with a latency (the degree of rotation of the phase arrows on the chart) that evolves over time. One explanation of this evolving latency is that since specific NFTs are popular during a relatively limited period of time where they are heavily traded, that these phase rotations reflect the transfer of an Ether account holding into the NFT and then later out of the NFT holdings. Additionally since NFT price increases with popularity, more Ether needs to be traded for each transaction. All of the 10 charts show almost a complete phase rotation over their trading life, reflecting the trade into, holding and trade out of that NFT.
-
OpenSea explains on their website that the average time it takes to process a transaction is around an hour. Additional time may be required for the ‘gas’ fees (transaction processing fees on the Ethereum blockchain) which are associated with an OpenSea transaction. Thus it is difficult for Ether-NFT portfolio balancing to take place in less that two hours.
-
NFTs experienced periods of frenzied trading (the red funnels in the charts) between one and about six times in their trading existence. Trading activity into and out of Ether occurred within 2 h (~ 128 min) and 8 h (~ 512 min) period cycles. Phase arrows show a trading from Ether into the NFT (rightward pointing arrows) and out of the NFT (rightward pointing arrows).
-
Trading platforms can be seen as a form of social media, with faddish trends directly impacted in prices. NFT trading behavior clearly indicates their faddish nature. NFT fads arise suddenly and arbitrarily, are quick-spreading and short-lived, quickly reversing themselves. In other social media, general novelty, mass marketing, peer pressure, and the desire to trendy drive interest and transactions. Furthermore, the NFT market is very thinly traded (see Figs. 1 and 2 on price and volume) with 99% of NFTs being traded less than 5 times. NFT markets like OpenSea have much more in common with social media platforms like TikTok, rather than with a liquid asset market like the New York Stock Exchange. TikTok is a short-form video hosting service owned by ByteDance. It hosts user-submitted videos, which can range in duration from 3 s to 10 min. Cloudflare ranked TikTok the World’s most popular website of 2021, surpassing Google.
Bitcoin
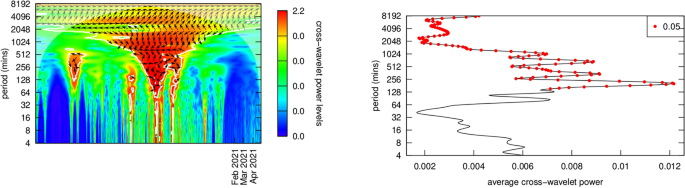
NFT-Bitcoin coherency is graphed in Fig. 14. Note that in Fig. 14, the x-axis time values show various ranges and are not consistent. These graphs do not all cover the same time period, but for the NFT-cryptocurrency coherency analysis this was not important, as only the periodicity of the NFT-cryptocurrency relationship is being elicited. Figure 14 presents the cross-wavelet coherency power spectra, revealing that observations made for the Ether-NFT coherency and trading patterns generally apply to Bitcoin-NFT coherency. Linkages between two markets are causal, in the mutual information sense of causality, and the direction of the causality is determined by whether phase analysis indicates a lead or lag relationship (the causal arrow has its arrowhead pointed to the lagging variable). The time-lag associated with the causal relationship is determined by the degree that the cycles are out of phase.
-
In a comparison of Ether-NFT coherency to Bitcoin-NFT coherency, we see trading (red funnels) taking place at roughly the same time and periodicity in and out of either Bitcoin or Ether, and at roughly the same cross-wavelet power levels (color legend on the right hand side).
-
Bitcoin trades seem to be taking place a bit faster (~ 1 h faster) than Ether trades, suggesting that computing ‘gas’ on the Ethereum blockchain may impose a time lag as suggested earlier.
Phase shifts
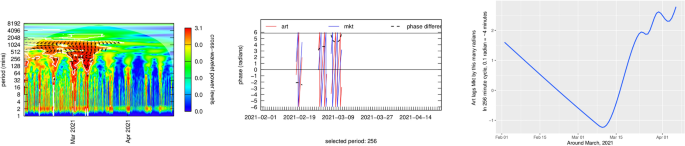
Figures 15 and 16 provide phase and power profiles for the two most heavily traded NFTs in the dataset, where I had sufficient data to compute these graphs. These graphs provide a more detailed explanation of the small directional arrows showing causal direction on the graphs in Figs. 12 and 14. “Phase” measures the relative time difference between two sinusoidal timeseries functions. The phase lag is one component of these functions and occurs when a system response lags behind a signal. The phase \(\omega\) information contained in the black arrows on analyses of the top 10 NFTs provides information about trading lead-lag times and direction. This is somewhat complicated to read from the charts since the period (y-axis) determines the exact timing. For example at a periodicity of 256 mins, a phase of \(\omega = \frac{\pi }{4}\) gives \(lag = \frac{\omega }{2\pi } \times period\) or 32 min. Since this information tends to be very time specific—it is not invariant across the entire period of trading in a specific NFT—it was felt that investigating the top two NFTs would be sufficient to review whatever additional information might be gleaned from detailed phase analysis. These figures display phase information for the Ether price stream and the first and second most traded NFTs. Each of these two figures shows the power curve (the red dots indicate which parts are statistically significant at the 5% level) a phase diagram (colors indicate the lead or lag in time in on a scale of \(\left[ { – \pi ,\pi } \right]\) minutes) and a phase lag chart for the period of most active trading for each particular NFT.
\(Ether – NFT_{rank1}\) analysis shows trading in ~ 1024 min periods where NFT price lags Ether price by about 8 radians \(\approx\) 1400 min (~ 1 day). Otherwise, there appear to be no linked price cycles in the two asset classes. \(Ether – NFT_{rank1}\) analysis shows trading in ~ 16, 128 and 512 min periods during the period January through August of 2020, during what was called the “crypto winter.” Period 16 showed showed almost no NFT price lags. Period 128 showed NFT price lags Ether price by about 5 radians in January 2020, or \(\approx\) 1 h. Period 512 showed NFT price lags Market price by about 5 radians in September 2020, or \(\approx\) 2 h, but by only around 10 min in early 2020. This, again, was a time of intense portfolio reassessment in the Bitcoin market, and that may have had an effect.
\(Ether – NFT_{rank2}\) analysis shows trading in ~ 512 min periods where NFT price leads Ether price by a rising trend of about 0 radians from 2-19-2021 through about 6 radians on 4-14-2021 (6 radians \(\approx\) 512 min (~ 8 h). Otherwise, there appear to be no linked price cycles in the two asset classes.
Interactions between the whole NFT market and individual NFTs
There is a tradition in asset market research of analyzing the influence of overall market sentiment on individual asset prices. The Capital Asset Pricing Model48 (CAPM) represents the most well-know of these approaches, and is used in separating risk into market and firm-specific risk (i.e., the so-called \(\alpha\) and \(\beta\)). In the current context I looked at the influence of the composite price movements of all NFT assets, versus individual price movements in the top traded three NFTs, and call these the NFT whole market effect.
Figures 17 and 18 analyzed price coherency between the most traded and second most traded NFT and the whole NFT market. Figure 19 provides power and coherency statistics for the influence of Whole NFT market influences on the second most traded NFT (the most traded NFT showed no phase lags at all, and thus the graph was noninformative for coherency). In looking at these, I have restricted the power spectrum graph to time periods in which there was active trading, and have placed arrows on the graph indicating the phase difference of the NFT vs. Market price series on a scale of \(\left[ { – \pi ,\pi } \right]\). At the far right of the figures is the power curve showing significant coherency power cycles. Figure 19 investigates high volume trading in one part of the second top NFT coherency power spectrum graph. The middle graph converts the arrows to a phase lag-lead on a scale of \(\left[ { – \pi ,\pi } \right]\) showing how the NFT and the market diverge. This divergence is isolated on the graph at the far right which shows the evolution of the lag-lead times for that particular short-term cycle.
This last bit of analysis is not generalizable, rather it represents detailed analysis of particular cases (a case study) of a single episode of very active trading. What it does reveal is a steady evolution of the informational lead to lag over about of frenzied trading. One can speculate that this in turn represents the diffusion of information, perhaps through forums and bulletin boards, of information and marketing for a specific NFT at a specific time. This is a rich potential area of investigation for future study.
This news is republished from another source. You can check the original article here